快排
天下武功，唯快不破!!外功如此，内功亦是如此。今日我们来修炼一门比较快速的排序算法-快速排序。快速排序流行的原因是它实现简单，并且在多数应用中比其他排序算法快的多。
习练快速排序，先要了解如下两个概念：
分治思想
关于排序，江湖盛传有一种分治思想,能大幅度提高排序心法的性能。所谓分治，即：化大为小，分而治之。达到治小而治大的成效。多年来基于分治思想衍生出多种排序心法，然万变不离其宗！
递归思想
关于递归，其实更像是一种解决问题的手段。我们把具有相同
解决思路的部分提取出来，循环调用。在code的表现形式上我们更倾向于说：自己调用自己。
虽然江湖上算法内功繁多，但是好的算法小编认为必须符合以下几个条件，方能真正提高习练者实力：
1
时间复杂度（运行时间）在算法时间复杂度维度，我们主要对比较和交换的次数做对比，其他不交换元素的算法，主要会以访问数组的次数的维度做对比。。
其实有很多修炼者对于算法的时间复杂度有点模糊，分不清什么所谓的 O(n),O(nlogn),O(logn)...等，也许下图对一些人有一些更直观的认识。
2
空间复杂度（额外的内存使用）排序算法的额外内存开销和运行时间同等重要。 就算一个算法时间复杂度比较优秀，空间复杂度非常差，使用的额外内存非常大，菜菜认为它也算不上一个优秀的算法。
3
结果的正确性这个指标是菜菜自己加上的，我始终认为一个优秀的算法最终得到的结果必须是正确的。就算一个算法拥有非常优秀的时间和空间复杂度，但是结果不正确，导致修炼者经脉逆转，走火入魔，又有什么意义呢？
原理 基本思想：选取一个元素作为分割点，通过遍历把小于分割点的元素放到分割点左边，把大于分割点的元素放到分割点元素右边。然后再按此方法对两部分数据分别排序，以此类推，直到分割的数组大小为1。 整个排序过程可以递归进行，以此达到整个数据变成有序序列。 实现快速排序的方式有很多，其中以类似指针移动方式最为常见，为什么最常见呢？因为它的空间复杂度为O（1），也就是说是原地排序
1. 我们从待排序的记录序列中选取一个记录(通常第一个)作为基准元素(称为key)key=arr[left]，然后设置两个变量，left指向数列的最左部，right指向数据的最右部。
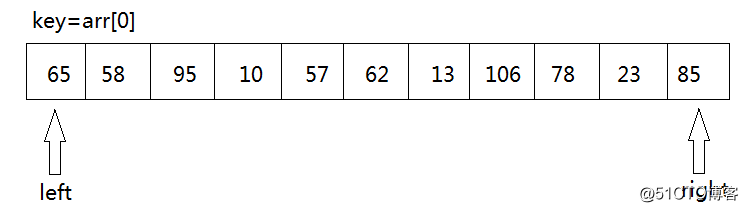
2. key首先与arr[right]进行比较，如果arr[right]<key，则arr[left]=arr[right]将这个比key小的数放到左边去，如果arr[right]>key则我们只需要将right--，right--之后，再拿arr[right]与key进行比较，直到arr[right]<key交换元素为止。
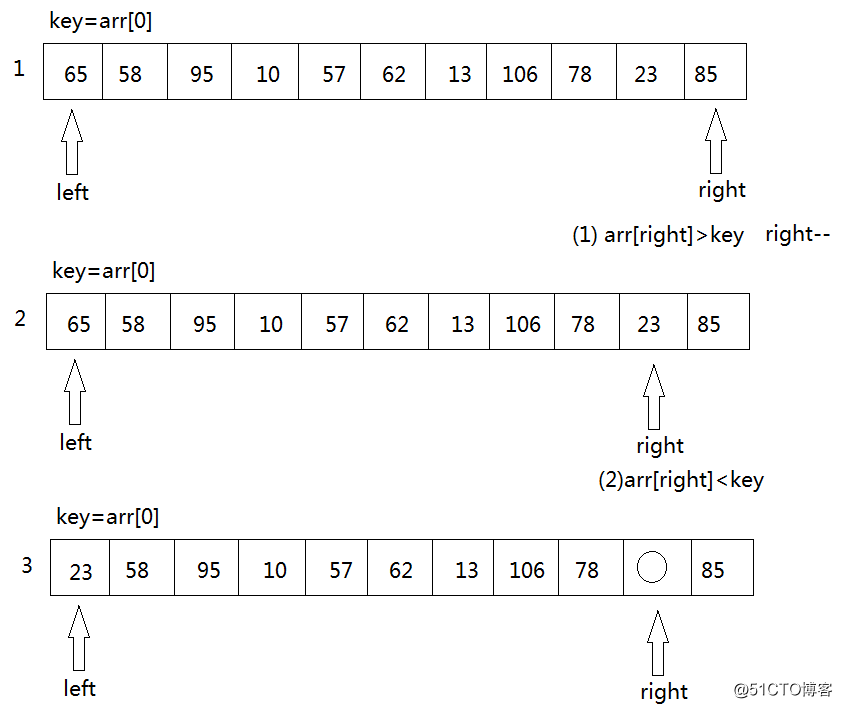
3. 如果右边存在arr[right]<key的情况，将arr[left]=arr[right]，接下来，将转向left端，拿arr[left ]与key进行比较，如果arr[left]>key,则将arr[right]=arr[left]，如果arr[left]<key，则只需要将left++,然后再进行arr[left]与key的比较。
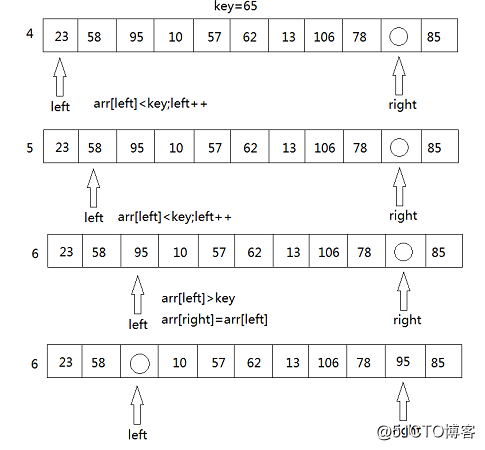
4. 然后再移动right重复上述步骤
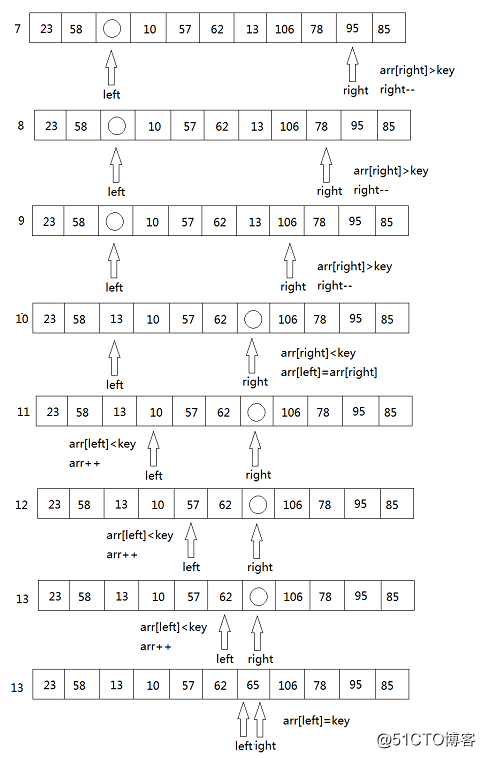
5. 最后得到 {23 58 13 10 57 62} 65 {106 78 95 85}，再对左子数列与右子数列进行同样的操作。最终得到一个有序的数列。
{23 58 13 10 57 62} 65 {106 78 95 85}
{10 13} 23 {58 57 62} 65 {85 78 95} 106
10 13 23 57 58 62 65 78 85 95 106
性能特点 关于复杂度相关O（n）等公式，我这里需要强调一点,公式代表的是算法的复杂度增长的趋势，而不是具体计算复杂度的公式。比如：O（n²）和O（n）相比较，只是说明 O(n²)增长的趋势要比o(n)快，并不是说明O(n²)的算法比O(n)的算法所用时间一定就要多。
1. 时间复杂度：
快速排序平均时间复杂度为O(nlogn),最好情况下为O(nlogn)，最坏情况下O(n²)
2. 空间复杂度：
基于以上例子来实现的快排，空间复杂度为O(1),也就是原地排序。
3. 稳定性：
举个例子：待排序数组:int a[] ={1, 2, 2, 3, 4, 5, 6};在快速排序的随机选择比较子(即pivot)阶段：若选择a[2]（即数组中的第二个2）为比较子，，而把大于等于比较子的数均放置在大数数组中，则a[1]（即数组中的第一个2）会到pivot的右边， 那么数组中的两个2非原序（这就是“不稳定”）。
若选择a[1]为比较子，而把小于等于比较子的数均放置在小数数组中，则数组中的两个2顺序也非原序。可见快速排序不是稳定的排序。
改进 通过以上分析各位侠士是否能够分析出来快速排序有哪些地方存在瑕疵呢？
1. 切分不平衡：
也就是说我们选取的切分元素距离数组中间值的元素位置很远，极端情况下会是数组最大或最小的元素，这就导致了划分出来的大数组会被划分为很多次。针对此情况，我们可以取数组多个元素来平衡这种情况，例如：我们可以随机选取三个或者五个元素，取其中间值的元素作为分割元素。
2. 小数组：
当快速排序切分为比较小的数组时候，也会利用递归调用自己。在这种小数组的情况下，其实一些基础排序算法反而比快速排序要快。当数组比较小的时候不妨尝试一下切换到插入排序。具体多小是小呢？一般5-15吧，仅供参考。
3. 重复元素：
在我们实际应用中经常会遇到重复元素比较多的情况，按照快排的思想，相同元素是会被频繁移动和划分的，其实这完全没有必要。我们该怎么办呢？我们可以把数组切换为三部分：大于-等于-小于 三部分数组，这样等于的那部分数组就可以避免移动了，不过落地的代码复杂度要高很多，有兴趣的同学可以实现一下。
使用场景1. 当一个数组大小为中型以上的数量级时，菜菜认为可以使用快速排序，并且伴随着数组的持续增大，快速排序的性能趋于平均运行时间。至于多大的数组为中型，一般认为50+ 吧，仅供参考。
2. 当一个数组为无序并且重复元素不多时候，也适合快速排序。为什么提出重复元素这个点呢？因为如果重复元素过多，本来重复元素是无需排序的，但是快速排序还是要划分为更多的子数组来比较，这个时候也许插入排序更适合。
试炼一发吧
1 c#武器版本
static void Main(string[] args) { List<int> data = new List<int>();
for (int i = 0; i < 11; i++)
{ data.Add(new Random(Guid.NewGuid().GetHashCode()).Next(1, 100)); } //打印原始数组值 Console.WriteLine($"原始数据： {string.Join(",", data)}"); quickSort(data, 0, data.Count - 1); //打印排序后的数组 Console.WriteLine($"排序数据： {string.Join(",", data)}"); Console.Read(); }
public static void quickSort(List <int> source, int left, int right)
{
int pivot = 0;
if (left < right)
{ pivot = partition(source, left, right); quickSort(source, left, pivot - 1); quickSort(source, pivot + 1, right); } } //对一个数组/列表按照第一个元素 分组排序，返回排序之后key所在的位置索引 private static int partition(List<int> source, int left, int right) {
int key = source[left];
while (left < right)
{ //从右边筛选 大于选取的值的不动，小于key的交换位置 while (left < right && source[right] >= key) { right--; }
source[left] = source[right];
while (left < right && source[left] <= key)
{ left++; }
source[right] = source[left];
}
source[left] = key;
return left;
} 2 golang 武器版 import (
"fmt"
"math/rand"
)
func main() {
var data []int for i := 0; i < 10; i++ {
data = append(data, rand.Intn(100))
}
fmt.Println(data)
quickSort(data[:], 0, len(data)-1)
fmt.Println(data)
}
func quickSort(source []int, left int, right int) {
var pivot = 0
if left < right {
pivot = partition(source, left, right)
quickSort(source, left, pivot-1)
quickSort(source, pivot+1, right)
}
}
func partition(source []int, left int, right int) int {
var key = source[left] for left < right {
for left < right && source[right] >= key {
right--
}
source[left] = source[right]
for left < right && source[left] <= key {
left++
}
source[right] = source[left]
}
source[left] = key
return left
}
运行结果：
[81 87 47 59 81 18 25 40 56 0][0 18 25 40 47 56 59 81 81 87]